1、※.曲线方程的定义域曲线方程表达式为y=e^(2x+y),即y>0,且lny=2x陴鲰芹茯+y,则:2x=lny-y.设2x=F(y)=lny-y,把y看成自变量,求导得:F'(y)=(1/y)-1=(1-y)/y.

2、有函数的导数单调性,计算隐函数的定义域。

3、计算函数的一阶导数,通过函数的一阶导数,进而判断函数的单调性。

4、曲线方旯皱镢涛程的单调性为:(1).当y∈(0,1]时,y'>0,此时曲线方程y随x的增大而增大;(2).当y∈(1,+∞)时,y'<0,此时曲线方程y随x的增大而减小。

5、 函数的凸凹性性,计算该隐函数的二阶导数,通过函数的二阶导数的符号,判断函数的凸凹性,并求解函数y的凸凹区间。

6、曲线方旯皱镢涛程的凸凹区间为:(1).当y∈(0,1]时,y">0,此时曲线方程为凹曲线;(2).当y∈(1,+∞)时,y"<0,此时曲线方程为凸曲线。

7、列举函数五点图:函数上部分点解析如下表所示,横坐标和纵坐标。

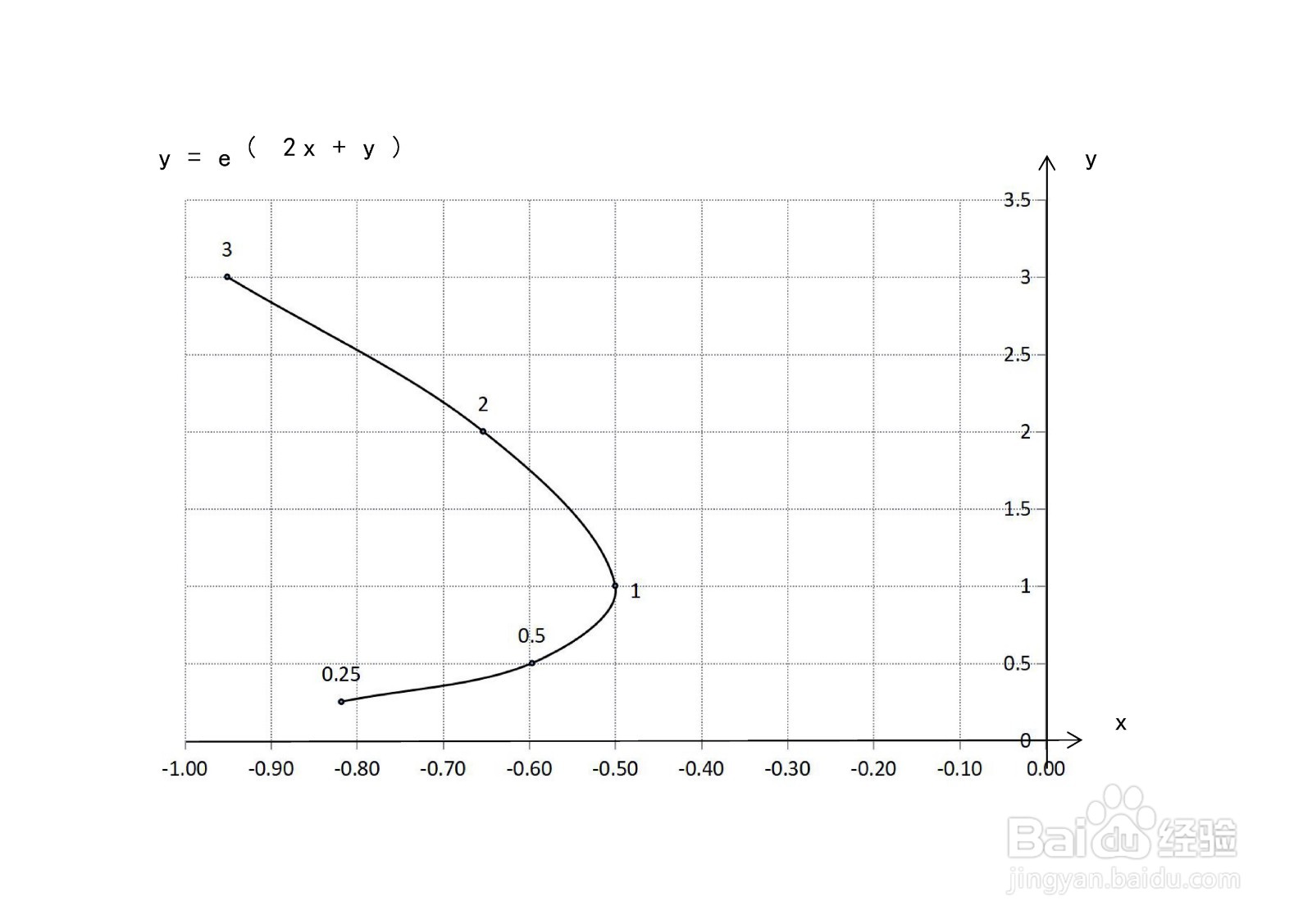
8、 根据曲线隐函数的定义域、值域、单调性、凸凹性和极限等性质,函数的示意图如下: